Computer Graphics Rendering in WebGL

Published Oct 5, 2023

Introduction

Many many individual pixels present on your device’s screen take on different colors to form shapes and letters in the big picture. However, everyone has interacted with some form of ‘3D’ graphics. Various games and simulations are capable of using our 2D screen to displaying 3D objects in a realistic manner. But how? How do graphics software like blender render such objects?

Prerequisites

• High school Calculus
• High school Linear Algebra (vectors, matrices, dot and cross products)
• High school Optics
• Basics of programming

Rasterization

When rendering an object to the screen, it essentially boils down to calculating which pixels to toggle at which color. Rasterization is the process of rendering polygons. Simple shapes are easy to calculate and, when many of them are put together to approximate a more complex object, produce detailed graphics.

Rasterization is easily the most prevalent rendering method. It has many benefits:

• Computationally inexpensive, don’t need high end graphics card
• Fast, can run in real-time
• Easily scalable in graphics quality
• Still able to produce very detailed rendering

Its most important strength is being computationally inexpensive. Most computers in the world don’t have the luxury of using anything slower.

Triangularization

In rasterization, most of the polygons used are triangles. All polygons can be split into triangles, after all. The process of approximating complex scenes with triangular meshes is Triangularization. An important benefit of using triangles is that they are always convex.

This isn’t just used for rasterization. We can also apply triangularization in algorithms like ray-tracing. The simulated geometry will be similarly rough, but the detail in computed lighting will be better.

The detail of an object depends, of course, on how much triangles are used to approximate it. Nowadays, engines even support dynamic triangularization, where rougher objects are approximated using a small amount of triangles and more are allocated to approximate intricate objects. This saves a lot of computation.

Rendering The Triangle

Rasterization projects the triangle onto the screen mathematically, then checks relevant pixels to determine which ones are contained in the triangle. These display the corresponding color and when combined together, form an entire image.

We can optimize the process in many ways, for example by only checking the pixels within the bounding box of the triangle.

Z-Dimension

However, it’s important to remember we are still in 3D-space. The extra dimension naturally brings about the problem of how to deal with overlaps. The process of determining which object should be rendered on top is called Backface Culling.

The most natural solution is to sort the objects by depth, or distance to the camera. This is called Painter’s Algorithm, but it runs into complications. What if three objects cyclically overlap each other?

Newell’s Algorithm can be used to eliminate these problems. Modern implementations have more sophisticated culling methods.

A Tangent: Seperating Axis Theorem

Determining if two polygons intersect or not is an obvious question of significance. One simple but very powerful observation is that: Two convex polgyons are seperate if and only if there is a line seperating them. The usefulness of the convexity of triangles is made clear here.

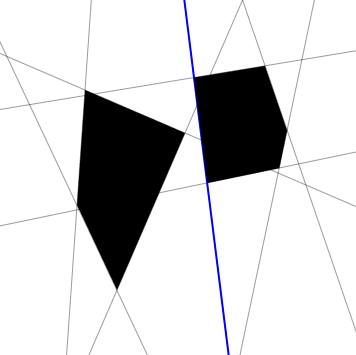
One solution is then to check all the edges of the polygon to see if they act as seperating axis. Another solution is to project all the vertices of the polygons onto a line, and see if the ranges of vertices intersect or not.

Here is an implementation of SAT.

Raytracing

Rasterization, however, is a mere approximation, using polygons. But it is important to note that the best we can do with graphics are approximations. The infinite detail of nature is impossible to simulate completely. We can, however, implement more accurate approximations.

Instead of approximating objects with polygons, raytracing actually simulates the nature of how we see.

Optics

So how do we actually see?

Every visible object is part of a dynamic exchange of light. Objects don’t emit light by themselves (unless they are light sources like the sun or a lamp); instead, they reflect it. When light from a source strikes an object, the object absorbs some wavelengths of light and reflects others.

The color of an object is determined by the wavelengths of light it reflects. For example, a red apple reflects red wavelengths and absorbs others. This reflected light, carrying information about the object’s color and brightness, then makes its way to our eyes.

We can't implement this!

Many light rays are reflected off of objects, and only a tiny fraction of them make their way to our eyes. We would waste an immense amount of computation on computing ‘useless’ rays.

Laser Eyes

Instead, we shoot rays from our camera (simulated eyes) to objects, each of which will (minus shadows) correspond to a unique ray from the light source. We’ll shoot one for each pixel in the screen to determine which color that pixel should be.

We’ll then need to calculate where the light ray will hit an object in the scene and color the pixel according to that intersection point’s exposure to the light source.

The Phong Model

Once we find an intersection, how exactly do we know what to color the pixel? There are many many factors that go into this, but we take a look at a basic model for today:

The Phong Reflection Model combines three types of lighting:

• Ambient Lighting
• Diffuse Lighting
• Specular Lighting

Ambient Lighting

This is the general light that’s present in a scene, even in the shadows. It’s like the soft light that fills a room even when the main lights are turned off. In the Phong Model, ambient light ensures that no part of the object is completely dark.

Simply give everything a base color, such as vec3(1.0, 1.0, 1.0) (white). It’s standard to normalize RGB values from 0-255 to the range 0-1.0.

Diffuse Lighting

Imagine a sunny day where light hits an object and spreads out in many directions, lighting the object evenly. This scattering of light is called diffuse reflection. It’s what makes objects visible from various angles and gives them their basic color.

To implement this, take the dot product of the light vector and the normal vector at that point on the object’s surface. The normal vector for raytraceable objects can be determined through explicit formulas (we can mathematically calculate the normal at any point on various objects, like a sphere). If they can’t, we’ll see later on how to approximate those.

We have the formula

float diffuse = max(0.0, dot(normal, light))}

Specular Lighting

Ever noticed how shiny objects have bright spots where light seems to sparkle? That’s the result of specular reflection. It’s the focused reflection of light that creates highlights on the surface of objects. In the Phong Model, this is what makes objects appear shiny.

We reflect the direction vector across the normal find the reflected vector

vec3 reflected = reflect(direction, normal)

Then we find the specular highlight by taking the dot product of the reflection and the light ray, to some exponent of shinyness, called the specular exponent. Depending on the object material, the higher the exponent, the shinier the highlight.

float specular = pow(max(dot(reflected, light), 0.0), SPECULAR_EXP)

Combination

The Phong Reflection Model combines these three types of lighting to create a balanced and realistic image. Ambient light fills in the shadows, diffuse reflection gives objects their base color, and specular reflection adds the finishing touch with highlights. It’s like a recipe for light that helps computer graphics look more lifelike.

The Cost of Intersection

We need to find intersection point of light rays and objects for Raytracing to work, and we model rays using vectors. But how exactly and where would vectors intersect an object?

Let’s take an extremely simple case. We work in 2D instead of 3D: where would the vectors intersect a very basic shape, a circle?

Circle Line Intersection

Let’s calculate the intersection of line through distinct points $(x_1, y_1) \not = (x_2, y_2)$ with a circle centered at the origin with radius $r$.

If we write

The points of intersection could be given as:

Isn’t this so complicated? And this is only for the most basic shape, a circle, at the origin, and even in 2D! These formulas may not be so computationally expensive for a computer, but they are hard to derive. Many objects don’t have the luxury of standard intersection formulas.

Distance Estimation

Here’s another problem, then. Given a point $P = (x, y)$ (camera) and a circle at $Q = (a, b)$ with radius $r$, find the distance to the circle.

Much simpler. Can we use the fact that, for basically all objects, the distance to a point is much easier to calculate than an explicit intersection with a line?

Volumetric Raytracing

Raytracing is quite impossible in many cases where the objects have very complicated intersection formulas (if you can derive any at all). But we can use the fact that distance is usually substantially easier to our advantage!

Here’s the algorithm for Volumetric Raytracing, often called Raymarching:

Raymarching Algorithm

• Start at the camera and point a ray towards some pixel $P$. We want to find the intersection point of a ray through $P$ with the scene.
• Find the distance $d_0$ to the nearest object.
• Move toward the direction of $P$ with length $d_0$.
• Find the new distance $d_1$ with the scene from your current point, and move in the same direction with distance $d_1$.
• Repeat until the distance towards the nearest object is less than some small value $\epsilon$, in which case we consider it an intersection. Your resulting position is the intersection point!

If after a large amount of iterations, we don’t get an intersection (distance doesn’t go below $\epsilon$), we know the ray simply misses all of the objects, and we can render some background color instead.

Here’s a visualization:

We started at the top left red dot. Each blue circle is a distance-finding step in the process. We found the distance to the nearest object and moved along the ray (black line) with that distance, to the next red dot. Ultimately, the red dots slowed down and the distance became smaller than $\epsilon$, meaning we hit an object (the black circle).

Shading

After finding the intersection point using raymarching, we can apply Phong shading as normal, with one problem: the normal vector. Often, an object not having an explicit intersection formula for raytracing means it also doesn’t have a formula for finding the normal vector at some point on its surface.

Calculus can save us! As long as we know the distance to the raymarch object, we can find the normal through the gradient

On the right, partial derivative can be approximated using the distance estimation formula we have for Raymarching. Usually, we normalize the gradient, so we can get rid of the denominator.

Partial derivative with respect to x_1 = DE(p + vec3(EPSILON, 0, 0)) - DE(p - vec3(EPSILON, 0, 0))

Shadows

Upon collision with an object in the scene, simply raymarch back to the light source, checking if there’s any collision in the process. If there is, an object obstructs the light from directly shining here, so you can shade the pixel black. This is a hard shadow. In reality, especially on the perimeter, shadows aren’t fully black. They appear fuzzy. This is because light sources aren’t points in space. Light sources themselves have volume, and this makes the edges slowly blur from dim to light. There are many ways to implement soft shadows, which take this into account. You can average the local neigborhood of pixel shadows, factor in the distance to the obstruction, etc.

Implementation and Beyond

See my CERXA Engine for an implementation of Volumetric Raytracing with some fractals to demo.

Here are a few resources I recommend if you want to learn more.

• Shadertoy
• Inigo Quilez
• Scratchapixel
• Syntopia

Configurating WebGL

You can implement the algorithms in this blog in many different environments. For reference, here is a basic boilerplate setup for WebGL in Vanilla HTML/JS:

index.html

<canvas id = "my-canvas"> <!-- Canvas that you will render output to -->
    Your browser does not currently support HTML5.
</canvas> 

<!-- Your vertex and fragment shader(s). These are written in GLSL. -->
<script id = "vertex-shader" type = "vertex-shader">
    // Shader code here ...

    void main(){

    }
</script>
<script id = "fragment-shader" type = "fragment-shader">
    // Shader code here ...

    void main(){

    }
</script>

<!-- Main Javascript script -->
<script src = "main.js"></script>

main.js

// Returns the WebGLRenderingContext from the desired canvas element
function initializeWebGL(canvas){
    const canvasElement = document.getElementById(canvas);

    if (!canvasElement || canvasElement.tagName !== "CANVAS"){
        throw new Error("Invalid canvas element or ID.");
    }

    // Get WebGL contest (OpenGL ES 2.0/3.0)
    // See all configurable context attributes here:
    // https://developer.mozilla.org/en-US/docs/Web/API/HTMLCanvasElement/getContext 
    let WebGLContext = canvasElement.getContext("webgl", 
    { /* Context attributes here */});

    if (!WebGLContext){
        throw new Error("Your browser does not currently support WebGL.");
    }

    return WebGLContext;
}

let gl = initializeWebGL("my-canvas");

// Creates a WebGL shader from a shader source
function createShader(gl, type, source){
    let shader = gl.createShader(type);
    
    gl.shaderSource(shader, document.getElementById(source).text);
    gl.compileShader(shader);

    if (gl.getShaderParameter(shader, gl.COMPILE_STATUS)){
        console.log("Successfully created shader of type: " + 
        (type === gl.VERTEX_SHADER ? "VERTEX_SHADER" : "FRAGMENT_SHADER"));
        return shader;
    }

    console.log("Failed to compile shader. Logs are shown below: \n");
    console.log(gl.getShaderInfoLog(shader));

    gl.deleteShader(shader);

    // throw new Error("Failed to compile shader");
}

// Creates a WebGL program with one vertex shader and one fragment shader
function createProgram(gl, vertexShader, fragmentShader){
    let program = gl.createProgram();

    console.log("Attaching shaders...");

    gl.attachShader(program, createShader(gl, gl.VERTEX_SHADER, vertexShader));
    console.log("Successfully attached vertex shader with source "  + 
    gl.getShaderSource(createShader(gl.VERTEX_SHADER, vts)));

    gl.attachShader(program, createShader(gl, gl.FRAGMENT_SHADER, fragmentShader));
    console.log("Successfully attached fragment shader with source "  + 
    gl.getShaderSource(createShader(gl.FRAGMENT_SHADER, fts)));

    gl.linkProgram(program);
    
    // Check if program linked successfully
    if (gl.getProgramParameter(program, gl.LINK_STATUS)){
        console.log("Sucessfully created program");
        return program;
    }

    console.log("Failed to create program. Logs are shown below: \n");
    console.log(gl.getProgramInfoLog(program));

    gl.deleteProgram(program);

    // throw new Error("Failed to create program");
}

let program = createProgram(gl, "vertex-shader", "fragment-shader");
gl.useProgram(program);

// Viewport resize with custom dimensions
function resize(gl, width = window.innerWidth, height = window.innerHeight, isSquare) {
    const minimumDimension = Math.min(width, height);

    // 1:1 canvas aspect ratio
    [gl.canvas.width, gl.canvas.height] = 
    isSquare ? [minimumDimension, minimumDimension]:[width, height];

    gl.viewport(0, 0, gl.canvas.width, gl.canvas.height);
};

resize(gl);

// Clear the color buffer
function clearColor(gl){
    gl.clearColor(0, 0, 0, 0);
    gl.clear(gl.COLOR_BUFFER_BIT);
}

clearColor(gl);

/** 
 * OpenGL stuff here...
 * 
 * Buffers
 * 
 * Uniform variables
 * 
 * etc...
*/

// The FPS to render at
const FPS = 60;

const startTime = performance.now();

function draw(){
    let currentTime = performance.now();

    // Draw OpenGL stuff here...
    // ...

    // Pass in elapsed time as a variable to the shader, useful for animated scenes
    gl.uniform1f(timeL, (currentTime - startTime)/1000); 
    
    window.requestAnimationFrame(draw, 1000/FPS);
}

// Start drawing when the page "load"s
window.addEventListener("load", draw, false);